1º ANO - APOSTILA - GEOMETRIA: CONCEITOS INICIAIS, TRIÂNGULOS E POLÍGONOS

Obs.: Para ter mais opções de impressão, e necessário que você:
1º Baixe o arquivo para  o PC e o salve;
2º Abra o arquivo baixado e salvado;
3º Mande imprimir FRENTE e VERSO, com propriedade de "virar as paginas impressão de livretos"

3ºI2 - REVISÃO - CILINDRO, CONE E ESFERA

01.    Um chapéu de festa feito de cartolina tem o formato de um cone reto e as dimensões indicadas na imagem.

Quantos centímetros quadrados de cartolina são necessários para produzir 50 unidades desse chapéu?

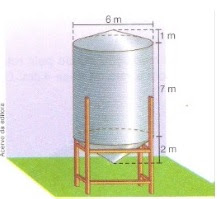
02. O esquema seguir representa um silo de armazenamento de grãos completamente cheio de soja. Considerando que cada metro cúbico dessa soja corresponda a 700 kg, calcule quantas sacas de 50 a Kg de soja correspondem a quantidade armazenada no silo.

03. O planeta Terra tem a forma aproximada de uma esfera com volume de 1 100 bilhões de quilômetros cúbicos. Dessa maneira, qual é o raio aproximado da Terra?

04.  Os bombons de chocolate esféricos, fabricados por uma indústria, tem seu interior um recheio que também possui forma esférica. Na imagem abaixo está representado um corte meridional nesse bombom. Qual é o volume de chocolate utilizado na produção de cada um desses bombons?

3ºI2 -       EXERCÍCIOS PROPOSTOS - LINK - ARQUIVO EM PDF

01.   Quantos litros de gás pode conter um reservatório industrial em formato esférico e com raio interno 2 m? (use p = 3,14).

02.   A superfície de uma bolha de sabão, de formato esférico tem 36p cm² de área. Qual é o volume de ar contido nessa bolha?

03.   O raio de uma esfera mede 4 cm. Um plano que seciona essa esfera determina nela um circulo com raio 1 cm. Determine a distância do plano ao centro da esfera.

04.   Calcule o volume de uma esfera, sabendo que a área de sua superfície é igual a 576π cm².

05.   Um plano intercepta uma esfera a uma distância do centro igual à medida do raio da seção que ele determina na esfera. Sabendo que o raio da esfera mede 4 cm, determine:

a)    A área da seção;

b)    A área do círculo máximo dessa esfera;

c) A área da superfície esférica.

EXERCÍCIOS DE REVISÃO - MATRIZES E DETERMINANTES - LISTA 2

EXERCÍCIO COMPLEMENTAR  - MATRIZES - LISTA 1

LISTA DE EXERCÍCIOS EM PDF - LINK

EXERCÍCIOS DE REVISÃO – (FAZER NO CADERNO 1 a 11)

01.  Escreva uma P.A. de 5 termos em que o primeiro termo é – 12 e a razão é r = 3.

02.  Escreva uma P.G. de 7 termos em que o primeiro termo é 10 e a razão q = √3

03.  Uma P.A. tem a₁ = 10 e r = 5. Determine a soma dos seus:

a) 20 primeiros termos;

b) 101 primeiros termos;

04.  Calcule a soma da P.A. (6 + 8 + 10 + ... + 84).

05.  Insira 10 meios aritméticos entre 30 e 74.

06.  Ache a₁ numa P.A de razão r = 10 e a₈₁ = 815.

07.  Numa progressão aritmética, o quinto termo e igual a 22 e o décimo termo e igual a 47. Calcule o primeiro termo e a razão dessa progressão.

08.  Determine o 12º termo da P.G. (5, 10, 20, ...).

09.  Interpole quatro meios geométricos entre 10 e 320.

10.  Encontre a₁ na P.G., sendo q = 3  e a₇ = 7290.

11. Numa P.G de q = 10 o a₁ = 100 e a_n = 1 000 000 000, qual é o valor de n?

APLICAÇÕES DE P.A – EXERCÍCIOS PROPOSTOS - 1 A 11

2º ANO - APOSTILA - MATRIZES E DETERMINANTES - PDF

2º ANO - EXERCÍCIOS DE REVISÃO - PDF

Lista de Exercícios de revisão - Arquivo PDF

2º ANO - EXERCÍCIOS DE REVISÃO

01.   Em certa região, a temperatura média mensal, em grau Celsius, varia de acordo com a lei f(t) = 26 +12.cos(π/6).t, em que t é medido em mês. Calcule a temperatura para esta região no mês de agosto.

02.   (PAEBES TRI – 2015) O gráfico que representa a função trigonométrica f(x) = sen (2x), definida de IR em IR é:

03. (PAEBES TRI – 2015) A temperatura média semanal T, em ºC, em uma determinada região durante o período de um ano, é expressa em função do tempo t, contado em semanas a partir da primeira semana do mês de janeiro, por meio da função T(t) = 10 + 12. Sen [2π.(t+10)/52)],  para 0 ≤ t ≤ 52. Nessa região, em que mês a temperatura média semanal foi máxima?

a) Janeiro.                    b) Abril.                         c) Julho .           d) Outubro.                  e) Dezembro.

04.   (Unesp-SP) Uma maquina produz diariamente x dezenas de certo tipo de peças. Sabe-se que o custo de produção C(x) e o valor de venda V(x) são dados aproximadamente, em milhões de reais, respectivamente, pelas funções: C(x) = 2 – cos (x.π)/6 e V(x) = 3√2.sen(x.π)/12, 0 ≤ x ≤ 6. O lucro, em reais, obtido na produção de 3 dezenas de peças é:

a) 500                          b) 750                          c) 1 000                        d) 2 000                        e) 3 000

05.   (PAEBES TRI - 2015) A Quantidade Q de energia solar média semanal que atinge uma determinada região, em Kcal/cm², durante o período de um ano, é expressa em função do tempo t, contado em semanas, por meio da função Q(t) = 300 + 200 . sen [2π. ((t-4)/12)]. A quantidade mínima de energia solar média semanal que atinge essa região, em Kcal/cm², é:

a) 100                          b) 200                           c) 300                           d) 500                          e) 700

06.   (PAEBES TRI – 2015) Observe a equação trigonométrica:

 Qual é o conjunto solução dessa equação?

07.   Determine o domínio das funções:

a) y = tg (x - 20º)

b) y = tg (x + 2π)

08.   Dê o conjunto solução da equação trigonométrica: sen(x) = -1/2.

09.   Construa o gráfico das funções, dando o domínio, a imagem e o período.

a) f(x) = 1  - 2 . sen x

b) y =  3 - cos x

3º ANO - GEOMETRIA - EXERCÍCIOS PROPOSTOS - LISTA 1

1º ANO: FUNÇÃO: EXERCÍCIOS DE REVISÃO - LISTA 1

2º ANO - LISTA DE EXERCÍCIOS - CIRCUNFERÊNCIA TRIGONOMÉTRICA - LISTA 1

ATIVIDADE AVALIATIVA

01.   Um capital de R$ 7.000 foi aplicado a juros compostos, durante um ano e meio, à taxa de 2,5% a.m. Calcule o montante e os juros auferidos no período.

02. Um capital de R$ 3.000 foi aplicado a juros compostos, durante 10 meses, gerando um montante de R$ 3.480. Qual a taxa mensal?

03. João Aplicou um capital de R$ 400,00 a juros compostos, durante três meses à taxa de 20% a.m. Calcule o montante e os juros obtidos no período.

Dados: [Use: (1,1)⁶ = 1,7716; (1,035)¹² = 1,5111; (1,025)¹⁸ =1,5597; (1,06)⁵ = 1,3382; (1,07)⁸ = 1,7182; (1,008)⁶ = 1,0490; (1,03)¹² = 1,4258; (1,055)⁴ = 1,2388;  ⁴√1,21 = 1,05; ¹⁰√1,16 = 1,0150].

EXERCÍCIOS DE REVISÃO 

01.   Calcule os juros e o montante de uma aplicação financeira a juros compostos, nas seguintes condições:

a)      Capital: R$ 10 000,00; taxa: 0,8% a.m; prazo: 6 meses;

b)      Capital: R$ 4 050,00; taxa: 3% a.m; prazo: 1 ano;

c)   Capital: R$ 500,00; taxa: 5,5% a.a; prazo: 4 anos;

02. Calcule o montante de um capital de R$ 6.000,00, aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês.

  

03.   Durante quanto tempo um capital deve ser aplicado a juros compostos, à taxa de 2,2%, para que duplique? (Use as aproximações: log 2 = 0,32 e log 1,022 = 0,01).

04.   Calcular o valor do montante final da aplicação de R$ 300.000,00 à taxa composta de 6% ao mês, durante 5 meses.

a) R$ 303.337,67                          c) R$ 401.460,00                            e) R$ 501.565,65

b) R$ 501.433,67                          d) R$ 601.457,65

05. Após 8 meses de aplicação a 7% ao mês de juros composto, o capital acumulado era igual a R$ 1.718.200,00. Qual o valor do capital aplicado?

a) R$ 800.001,78                         c) R$ 763.301,33                             e) R$ 1.000.000,00

b) R$ 789.661,78                         d) R$ 1.069.996,20

06. Durante quanto tempo um capital de R$ 1.000.000,00, a juros compostos, a uma taxa de 15% a.a., produzirá um montante de R$ 2.011.356,00? (Use: log 2 = 0,30 e log 1,15 = 0,06).

a) 5 anos ‘                                c) 6 anos                                  e) 7 anos

b) 4 anos                                  d) 3 anos

07.  O capital R$ 5.000,00 foi aplicado a juros compostos durante 4 meses. Ao final do prazo o montante será igual a R$ 6.050,00. Qual a taxa da aplicação? 

a) 9% a.m.                              c) 7% a.m.                               e) 5% a.m.

b) 8% a.m.                              d) 6% a.m.

1º ANO: EXERCÍCIOS COMPLEMENTARES

MATUTINO - TRABALHO: MATEMÁTICA FINANCEIRA -2ºM1 E 2ºM2

GRUPOS DE TRABALHO COM NOMES E TEMAS - 2ºM1 - 2ºM2


VESPERTINO - TRABALHO: MATEMÁTICA FINANCEIRA - 2ºI1- 2ºV1 - 2ºV2 - 2ºV3

GRUPOS DE TRABALHO COM NOMES E TEMAS - 2ºI1 - 2ºV1 - 2ºV2 - 2ºV3

1º ANO - EXERCÍCIOS DE FIXAÇÃO - LINK PARA DOWNLOAD

2º ANO - EXERCÍCIOS DE REVISÃO

ARQUIVO EM PDF - LINK PARA DOWNLOAD

EXERCÍCIOS DE REVISÃO

01.   A mensalidade de um curso de Inglês no mês de setembro era R$ 120,00. No mês seguinte o valor da mensalidade sofreu um acréscimo de 9%. Qual era o valor da mensalidade após o acréscimo?

02.   Fernanda pagou R$ 375,00 em uma prestação do financiamento de seu carro, o que corresponde a 12% de seu salário. Calcule o valor do salário de Fernanda.

03.   Certo eletrodoméstico teve um reajuste de 3%, passando a custar R$ 590,00. Calcule o valor desse eletrodoméstico antes do reajuste.

04.   (FGV) Se uma mercadoria sofre dois descontos sucessivos de 15% e depois um acréscimo de 8%, seu preço final, em relação ao preço inicial:

a) aumentou de 22%                                                  d) decresceu de 23%

b) decresceu de 21,97%                                             e) decresceu de 24%.

c) aumentou de 21,97%

05.   Uma mercadoria que custa R$ 80,00 reais sofre um desconto de 60%. Um aumento de 60% sobre o novo preço fará com que a mercadoria fique custando, em reais:

a) R$ 28,80                                          c) R$ 48,00                           e) R$ 80,00.

b) R$ 32,00                                          d) R$ 51,20

                                   

06.   Simone fez uma aplicação no valor de R$ 1000,00 durante 7 meses, a taxa de juros simples de 0,65% a.m. Calcule o montante obtido por Simone ao final da aplicação.

07.   Sergio aplicou R$ 12 000,00 no sistema de juro simples e, após 10 meses, retirou o montante de R$ 12 900,00. Qual foi a taxa mensal de juro que rendeu o investimento de Sérgio?

08.   Um capital de R$ 860,00, aplicado a juro simples com taxa anual de 30%, após certo período de tempo resulta em um montante de R$ 989,00. Determine quantos meses esse capital ficou aplicado para obtenção desse montante.

09.   Júlio aplicou, sob regime de juro simples, a importância de R$ 7 500,00, com taxa de 2,5% a.m., por um período de dois trimestres.

a) Qual era o montante ao fim desse período?

b) Devido a pagamentos de impostos, o montante a ser retirado por Júlio sofrerá uma redução de 3%. Qual será o valor liquido retirado após esses investimentos?

1º ANO - CONCEITOS DE FUNÇÃO

EXERCÍCIOS DE REVISÃO

01.  Considere a função F: A à B representada pelo diagrama a seguir. Determine:

                         

        a) o domínio (D) de f;

        b) f(1), f(-3), f(3) e f2);

        c) o conjunto imagem (Im) de f;

        d) A lei de associação que forma a função.

02. Seja à função definida por f(x) = 2x – 4 determinem o valor de:

a) f(3) =                                      c) f(x) = 0

b) f(-5) =                                     d) f(x) = 10

03.    A distância percorrida por um automóvel, em uma viagem, é função do tempo. Suponha essa função seja dada pela equação: d = 80.t, onde d é a distância em km, e t o tempo, em horas. Se o percurso todo do automóvel, durante a viagem, foi de 400 km, quanto tempo durou essa viagem?

a) 2 horas                                b) 3 horas                               c) 4 horas

d) 5 horas                                e) 6 horas

04. Seja a função f(x) = 3x + 2. Determine f(0) e f(-2).

05.    Dada a função f: IR à IR definida por f(x) = ax + b, com a, b ϵ IR, calcular o valor de a e b, sabendo-se que f(2) = 20 e  f(3) = 25.

06. Verificar se os diagramas a seguir representam ou não, funções de A em B.

2º ANO: LISTA DE EXERCÍCIOS 1 - LINK PARA DOWNLOAD

2º ANO - EXERCÍCIOS DE REVISÃO - LINK PARA DOWNLOAD

2º ANO - EXERCÍCIOS COMPLEMENTARES

01.   A análise de uma cultura de bactérias registrou que existem, inicialmente 1 000 bactérias presentes e, após t minutos, a quantidade de bactérias é N(t) = 1 000 . 2^0,8.t

a) Verifique se, em 10 minutos, a quantidade de bactérias presentes na cultura será superior a 200 000?

b) Represente graficamente.

02. A população de peixes em um lago está diminuindo devido à contaminação de água por resíduos industriais. A lei n(t) = 5000 – 10.2^t–1 fornece uma estimativa do número de espécies vivas [n(t)] em função do número de anos (t) transcorridos após a instalação do parque industrial na região.

a) Estime a quantidade de peixes que viviam no lago após 3 anos da instalação do parque industrial.

b) Algum tempo após as indústrias começam a operar, constatou-se que havia no lago menos de 4 920 peixes. Para que valores de t vale essa condição?

EXERCÍCIOS DE REVISÃO - 1º ANO - CONJUNTOS NUMÉRICOS

01. (PUC) Numa comunidade constituída de 1800 pessoas há três programas de TV favoritos: Esporte (E), novela (N) e Humanismo (H). A tabela abaixo indica quantas pessoas assistem a esses programas.

Programas	Número de telespectadores
E	400
N	1220
H	1080
E e N	220
E e H	180
N e H	800
E, N e H	100
Nenhum	x

Através desses dados verifica-se que o número de pessoas da comunidade que não assistem a qualquer dos três programas é:

a) 200                                                                         d) 100

b) os dados do problema estão incorretos                      e) n.d.a

c) 900

02.    (Unifap) O dono de um canil vacinou todos os seus cães, sendo que 80% contra parvovirose e 60% contra cinomose. Determine o porcentual de animais que foram vacinados contra as duas doenças.

03.    (UFSE) Os senhores A, B e C concorriam à liderança de certo partido político. Para escolher o líder, cada eleitor votou apenas em dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C. Em consequência:

a) venceu A, com 120 votos.
b) venceu A, com 140 votos.
c) A e B empataram em primeiro lugar.
d) venceu B, com 140 votos.
e) venceu B, com 180 votos.

04.    Dez mil aparelhos de TV foram examinados depois de um ano de uso e constatou-se que 4.000 deles apresentavam problemas de imagem, 2.800 tinham problemas de som e 3.500 não apresentavam nenhum dos tipos de problema citados. Então o número de aparelhos que apresentavam somente problemas de imagem é:

a) 4 000            b) 3 700            c) 3 500            d) 2 800            e) 2 500

05.    Em uma prova discursiva de álgebra com apenas duas questões, 470 alunos acertaram somente uma das questões e 260 acertaram a segunda. Sendo que 90 alunos acertaram as duas e 210 alunos erraram a primeira questão. Quantos alunos fizeram a prova?

06.    Em uma escola foi realizada uma pesquisa sobre o gosto musical dos alunos. Os resultados foram os seguintes:

·         458 alunos disseram que gostam de Rock;

·         112 alunos optaram por Pop;

·         36 alunos gostam de MPB;

·         62 alunos gostam de Rock e Pop.

Determine quantos alunos foram entrevistados.

07.    Numa pesquisa sobre as emissoras de tevê a que habitualmente assistem, foram consultadas 450  pessoas, com o seguinte resultado: 230 preferem o canal A; 250 o canal B; e 50 preferem outros canais diferente de A e B. Pergunta-se:

a) Quantas pessoas assistem aos canais A e B?

b) Quantas pessoas assistem ao canal A e não assistem ao canal B?

c) Quantas pessoas assistem ao canal B e não assistem ao canal A?

d) Quantas pessoas não assistem ao canal A?

08.    Observe o diagrama e responda:

                                            Quais são os elementos dos conjuntos abaixo:

a) P =

b) Q =

c) R =

d) P∩Q∩R =

e) (P∩Q)  (Q∩R) =

f) (P∩R) Q=

g) P – Q =

                                            h) (P U Q) – R =

EXERCÍCIO DE REVISÃO EM ARQUIVO PDF - LINK PARA DOWNLOAD